Waren große Sprachmodelle wie ChatGPT anfangs noch für ihre mathematischen Schwächen bekannt, lösen sie heute komplexe Wettbewerbsaufgaben. Dieser Beitrag beleuchtet die rasanten Fortschritte von KI in der Mathematik.
Warum sind LLMs so schlecht in Mathe?
Zumindest bis ins Jahr 2023 waren Large Language Models (LLMs) wie ChatGPT oder LLaMA bei mathematischen Aufgaben wenig hilfreich. Während die Antworten durchaus sprachlich flüssig und sinnvoll klangen, wurde oftmals schräg argumentiert oder schlichtweg falsch gerechnet. Zwei Beispielfragen hierzu aus dem Cognitive Reflection Test von S. Frederick [1].
Frage 1: Wenn fünf Maschinen fünf Minuten brauchen, um fünf Produkte herzustellen, wie lange brauchen dann 100 Maschinen, um 100 Produkte herzustellen?
Eine spontane, aber falsche Antwort könnte etwa "100 Minuten" sein. Auch die folgende Lösung ist falsch.
Antwort von LLaMA-2-13B [2]:
Wenn fünf Maschinen fünf Minuten brauchen, um fünf Produkte herzustellen, bedeutet das, dass jede Maschine eine Minute braucht, um ein Produkt herzustellen. Bei 100 Maschinen benötigt jede Maschine eine Minute, um ein Produkt herzustellen. Somit benötigen alle 100 Maschinen eine Minute, um 100 Produkte herzustellen.
Die richtige Antwort lautet allerdings "5 Minuten".
Frage 2: In einem See befindet sich ein Seerosenbeet. Jeden Tag verdoppelt sich seine Größe. Wenn es 48 Tage dauert, bis das Beet den gesamten See bedeckt, wie lange würde es dann dauern, bis es die Hälfte des Sees bedeckt?
Antwort von LLaMA-2-13B:
Dies ist ein klassisches Beispiel für exponentielles Wachstum. Am 48. Tag bedeckt das Beet den gesamten See. Um herauszufinden, wie lange es dauern würde, bis das Beet die Hälfte des Sees bedeckt hätte, können wir die Tatsache nutzen, dass sich die Fläche jeden Tag verdoppelt. Wenn es also 48 Tage dauert, den gesamten See zu bedecken, dann würde es die Hälfte dieser Zeit (oder 48 / 2 = 24 Tage) dauern, bis die Hälfte des Sees bedeckt ist.
Obwohl das LLM richtigerweise "exponentielles Wachstum" erwähnt, scheitert es beim Berechnen der korrekten Lösung, welche nicht 24, sondern 48 − 1 = 47 Tage beträgt.
Das Scheitern von LLMs bei einfachen Mathematikaufgaben mag zunächst überraschend erscheinen, da ausgerechnet ein Computerprogramm beim Rechnen versagt. Allerdings folgen die Berechnungen eines LLMs einer inneren Logik des zugrunde liegenden neuronalen Netzes, und sind daher mitunter unsinnig bezüglich der von Menschen verstandenen Semantik.
Diesbezüglich lassen sich die Antworten eines LLMs mithilfe eines Modells des Psychologen Daniel Kahneman besser verstehen. Kahneman unterscheidet zwei Systeme menschlichen Denkens. System 1 ist intuitiv, automatisch und schnell. Es funktioniert assoziativ und nutzt erlernte Muster, etwa beim Erkennen von Gesichtern oder beim Vervollständigen von Texten. Die Heuristiken von System 1 sind einerseits extrem wertvoll, greifen sie doch auf unsere Erfahrungen und erlerntes Wissen zurück. Andererseits ist System 1 anfällig für zahlreiche Voreingenommenheiten und Fehleinschätzungen. (Leseempfehlung: Kahnemans Buch Thinking, Fast and Slow.)
Bei kleinen Rechenaufgaben wie 2+3 genügt System 1, zumindest bei Erwachsenen, die die Antwort auswendig kennen. Will ein Kind 2+3 berechnen, oder ein Erwachsener eine Aufgabe wie 19 · 57 im Kopf berechnen, so kommt System 2 zum Einsatz. Dieses arbeitet analytisch, logisch und mit höherem Zeit- und Energie-Aufwand. Wir nutzen es zum Argumentieren, Abwägen und zum Lösen komplexer Probleme.
Ein LLM lässt sich als ein System 1 verstehen, ein Pattern-Matcher, der eine gigantisch große Zahl an Assoziationen gelernt hat. Seine Antworten wirken flüssig und überzeugend, sind in erster Linie aber zu impulsiv für komplexeres analytisches Denken. In der Mathematik, bei der logische Präzision gefragt ist, wird diese Schwäche deutlich sichtbar.
Wieviel ist 19 · 57?
System-2-Antwort: Mit höchster Konzentration berechnen wir 19 · 57 = 10 · 57 + 9 · 57 = 570 + 513 = 1083.
System-1-Antwort: Eine Schätzung könnte etwa 19 · 57 ≈ 20 · 50 = 1000 sein. Wenn die Rechenaufgabe bekannt ist oder oft geübt wurde, könnte ein System 1 allerdings die Antwort 1083 auch automatisch abrufen.
Warum sind LLMs so gut in Mathe?
Mittlerweile schneiden LLMs bei mathematischen Aufgaben jedoch deutlich besser ab, wie die türkise Linie (Competion-level mathematics (MATH)) in folgender Grafik aus dem AI Index 2025 Annual Report [3] zeigt.
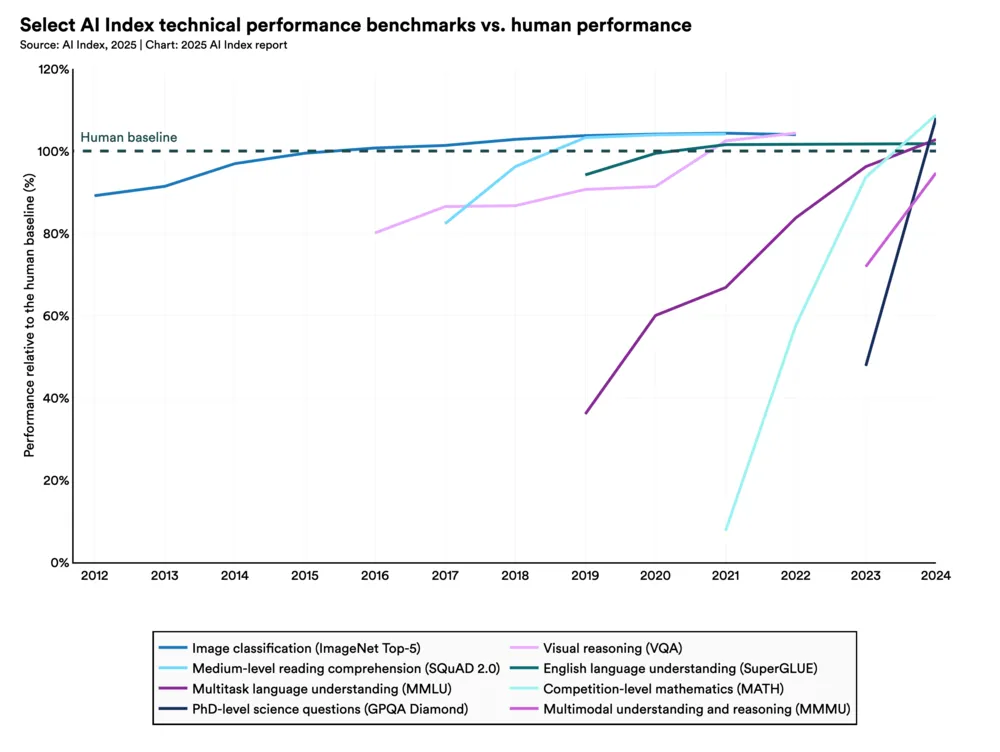
Grafik aus dem AI Index 2025 Annual Report [3], verwendet unter der Lizenz CC BY-ND 4.0.
Hierbei besteht die Mathematik-Benchmark aus Aufgaben aus Schulwettbewerben [4], zum Beispiel:
Aufgabe: Tom hat eine rote Murmel, eine grüne Murmel, eine blaue Murmel und drei identische gelbe Murmeln. Wie viele verschiedene Gruppen von zwei Murmeln kann Tom wählen?
Lösung: Es gibt zwei Fälle: Entweder wählt Tom zwei gelbe Murmeln (1 Ergebnis), oder er wählt zwei Murmeln unterschiedlicher Farbe, ( Ergebnisse). Die Gesamtzahl der unterschiedlichen Murmelpaare, die Tom wählen kann, beträgt .
Die rasante Leistungssteigerung von LLMs im Bereich Mathematik ist mindestens auf die folgenden zwei Ansätze zurückzuführen:
- Externes System 2: Da LLMs sehr gut in sprachlicher Mustererkennung sind, erkennen sie immerhin, wann ihnen eine mathematische Frage gestellt wird. Diese kann dann an externe Tools weitergeleitet werden – etwa an einen “Taschenrechner”, ein Computeralgebrasystem, ein Python-Programm o. Ä. In diesem Fall sucht sich das System 1 also Hilfe bei einem externen System 2. (Für diese Art des Austausches zwischen LLMs und externen Datenquellen scheint sich aktuell das Open-Source-Framework Model Context Protocol des Unternehmens Anthropic durchzusetzen.)
- Emuliertes System 2: Ein weiteres Konzept, das LLMs zu mehr Abwägung und analytischem Denken verhelfen kann, ist das Chain-of-Thought Prompting. Indem das LLM dazu angeleitet wird, schrittweise zu antworten und seine eigenen Zwischenergebnisse mittels Feedback-Schleifen zu hinterfragen, kann es deutlich reflektierter agieren und komplexere Probleme besser durchdringen. In gewisser Weise wird mit dieser Technik ein System 2 nachgeahmt.
Frage: Tom hat eine rote, zwei identische grüne, drei identische gelbe und drei identische blaue Murmeln. Wie viele verschiedene Dreiergruppen kann Tom wählen?
ChatGPT (o4-mini) liefert neben der abschließenden Antwort seinen Gedankengang zum Auffinden der Lösung:
Ich werde überlegen, wie viele Möglichkeiten es gibt, 3 Kugeln aus den gegebenen Farben (rot, grün, gelb, blau) unter Berücksichtigung der Farbgrenzen auszuwählen. Ich werde das mit einer Berechnung angehen, die entweder manuell oder durch ein kleines Programm zu lösen ist, um die Anzahl der Gruppen und damit die Antwort zu ermitteln.
Anschließend schreibt es ein Python-Programm, das durch Iteration die korrekte Lösung 15 liefert:
count = 0
triples = []
for r in range(0,2):
for g in range(0,3):
for y in range(0,4):
for b in range(0,4):
if r+g+y+b == 3:
count += 1
triples.append((r, g, y, b))
count, triples[:10]
Output:
(15, [(0, 0, 0, 3), (0, 0, 1, 2), (0, 0, 2, 1), (0, 0, 3, 0),
(0, 1, 0, 2), (0, 1, 1, 1), (0, 1, 2, 0), (0, 2, 0, 1),
(0, 2, 1, 0), (1, 0, 0, 2)])
Digitalisierung der Mathematik
Ein LLM bezieht sein Wissen über Mathematik ganz ähnlich wie Menschen aus Büchern, Vorlesungsskripten, wissenschaftlichen Artikeln, Forenbeiträgen etc. Allerdings ließe sich mathematisches Wissen auch grundsätzlich anders darstellen – digital und losgelöst von menschlicher Sprache. Die theoretischen Grundlagen der Informatik entwickelten sich historisch aus fundamentalen Fragestellungen zu Mathematik und Logik. Ironischerweise wurde die Mathematik selbst bislang nicht oder nur sporadisch digitalisiert.
Obwohl seit mehr als 100 Jahren mehrere sogenannte formale Sprachen für genau diesen Zweck entwickelt wurden – gewissermaßen Programmiersprachen für Mathematik – wurde mathematisches Wissen, d.h. Definitionen, Vermutungen, Sätze und Beweise, bisher nur ansatzweise in eine digitale Form gebracht. Eine Herausforderung besteht im enormen Aufwand, der mit dem Verfassen eines formalen mathematischen Textes verbunden ist. Solche Texte können extrem lang werden, da sie jeden noch so kleinen logischen Schritt explizit enthalten müssen.
Für eine Datenbank digitalisierter Mathematik – oder eines Teilbereichs wie Zahlentheorie, Schul- oder Universitäts-Mathematik – könnten Algorithmen entwickelt werden, die uns Menschen beim Lernen, Lehren und Forschen unterstützen. Im Artikel Die Digitalisierung der Mathematik wurde bereits auf Entwicklungen in diesem Bereich eingegangen, insbesondere auf ambitionierte Projekte rund um die jüngere formale Sprache Lean. Hier schreitet die Formalisierung in der Tat weiter voran: Im Juli 2023 wurde die Lean Focused Research Organization gegründet, um die “Formal Mathematics Revolution” voranzutreiben [5], und Kevin Buzzard wurde ein Forschungsstipendium bewilligt, mit dem Ziel, innerhalb von fünf Jahren den Beweis des Großen Fermatschen Satzes in Lean zu formalisieren [6]. Das von Terence Tao initiierte “Equational Theories Project” ist ein Beispiel für eine erfolgreiche Online-Zusammenarbeit, bei der rund 22 Millionen Implikationen zwischen algebraischen Gleichungen in Lean untersucht wurden [7]. Ein großer Vorteil besteht darin, dass die Kollaboration “trustless” ist – es wird also keine zentrale Vertrauensinstanz benötigt, um die Beiträge auf Gültigkeit zu überprüfen.
Das Lösen eines mathematischen Problems in formaler Sprache lässt sich mit einem Spiel wie Schach vergleichen: Auch in der Mathematik existieren klar definierte Spielzüge – logische Schlussfolgerungen, mit denen sich bekannte Aussagen in neue überführen lassen. Die korrekte und schrittweise Anwendung solcher Schlussfolgerungen ist eine typische System-2-Aufgabe, da eine Abfolge von Schritten erforderlich ist, um Axiome oder bereits bewiesene Sätze schlüssig und lückenlos in die Lösung des gegebenen Problems zu überführen. (Das eigentliche Auffinden eines geeigneten Lösungswegs hingegen beinhaltet durchaus kreative, intuitive Elemente – also Aspekte von System 1.)
Das zu Google gehörende Unternehmen DeepMind, bekannt durch die KIs AlphaGo, AlphaZero und AlphaFold, hat zu diesem Zweck im Jahr 2024 die KI AlphaProof entwickelt. AlphaProof übersetzt zunächst ein mathematisches Problem mittels des LLMs Gemini in Lean. Mathematisches Schlussfolgern hat sich AlphaProof ähnlich wie AlphaZero (Schach) durch Reinforcement Learning anhand von Millionen bekannter mathematischer Probleme selbst beigebracht. Das selbstgesteckte Ziel war die Bearbeitung der Aufgaben der Internationalen Mathematik-Olympiade (IMO) 2024. Die IMO ist ein internationaler Schülerwettbewerb, der seit 1959 jährlich stattfindet. Die Aufgaben dieses Wettbewerbs sind alles andere als einfach und erfordern ein hohes Maß an Kreativität. Die Lösungsvorschläge von AlphaProof erzielten 28 von 42 möglichen Punkten – was einer Silbermedaille entspricht. Eine Goldmedaille (mindestens 29 Punkte) wurde von weniger als 10 % der Teilnehmer erreicht. (Dabei wurden geometrische Probleme von AlphaGeometry, einer weiteren auf Geometrie spezialisierten KI von DeepMind, bearbeitet.) Ein Manko: Die Mathematikaufgaben wurden laut DeepMind zunächst von Hand formalisiert und erst in dieser Form AlphaProof übergeben [8].
Eine IMO-Goldmedaille für eine KI sollte schon bald kein Problem mehr sein, und größere Ziele werden bereits anvisiert, wie zum Beispiel die Benchmark FrontierMath für Mathematik auf Expertenniveau [9], [10]. (Erwähnenswert ist jedoch der Skandal, dass OpenAI zwar von einem 25%-Score für ihr o3-Modell berichtete, aber später bekannt wurde, dass OpenAI selbst an der Erstellung von FrontierMath beteiligt war [11].)
LLMs und der de-Bruijn-Faktor
Im Artikel [12] definiert F. Wiedijk den de-Bruijn-Faktor (benannt nach dem niederländischen Mathematiker Nicolaas Govert de Bruijn) als den Quotienten aus der Länge einer Formalisierung eines mathematischen Textes und der Länge des ursprünglichen, informellen Textes. Der Autor berechnet anschließend den de-Bruijn-Faktor für drei Beispieltexte, bei denen sich jeweils ein Wert von circa 5 ergibt.
Definieren wir den de-Bruijn-Faktor nun etwas praxisorientierter als den Quotienten zwischen dem (Zeit-)Aufwand für das Aufschreiben eines formalen und dem Aufwand für das Aufschreiben des entsprechenden informellen mathematischen Textes. In einem Vortrag vom Januar 2024 [13] schätzt Terence Tao diesen Faktor beispielsweise auf 10 bis 20. Dieser Wert wird jedoch umso kleiner sein, je mehr Formalisierungsvorarbeit bereits geleistet wurde. Zudem wird das Programmieren an sich seit der Einführung von ChatGPT durch LLMs unterstützt und teilweise stark beschleunigt. Auch für Lean existiert bereits ein entsprechendes LLM-Tool – der LeanCopilot [14].
Der de-Bruijn-Faktor wird in Zukunft sicherlich weiter sinken, und es stellt sich die interessante Frage, ob er (zumindest in einem Teilgebiet) sogar auf einen Wert unter 1 fallen könnte. In diesem Fall wäre das Aufschreiben eines formalen Beweises schneller als das eines informellen. Das Überprüfen des Beweises auf Korrektheit würde dann nur noch einen Mausklick erfordern.
Schon jetzt lässt sich aus einem Lean-Beweis ein primitives LaTeX-Dokument erstellen oder ein sogenannter Dependency Graph, der anzeigt, aus welchen anderen Theoremen ein Beweis hervorgeht. Es wäre anzunehmen, dass in einer solchen utopischen Zukunft das Erstellen eines für Menschen lesbaren Artikels dann ebenfalls auf Knopfdruck durch ein LLM geschehen könnte. Eine derartige Beschleunigung des Verifizierens, Publizierens und Kommunizierens von Mathematik könnte nichts weniger als einen Paradigmenwechsel bedeuten.
Lassen wir zum Schluss ChatGPT zu Wort kommen, welches unter anderem an folgende neuartige Fragestellungen denkt, die in einer KI-gestützten, formalisierten Mathematik-Zukunft auftauchen könnten:
- Automatische Entdeckung neuer Axiome: Kann ein KI-System durch Analyse großer Mengen formalisierten Wissens neue, konsistente Axiome vorschlagen, die bisher übersehene Strukturen in der Algebra oder Geometrie beschreiben?
- Formal verifizierte Datenanalyse-Pipelines: Wie kann man statistische Methoden und Maschinelles Lernen unter formal verifizierten Rahmenbedingungen implementieren, sodass jedes Ergebnis in wissenschaftlichen Studien automatisch auf mathematische Korrektheit geprüft wird?
- KI-gestützte Beweisnähe-Analyse: Wie kann man formale Beweisbibliotheken analysieren, um mithilfe von KI-Systemen Engpässe und Lücken in der mathematischen Literatur aufzuspüren und gezielt neue Forschungsvorhaben vorzuschlagen?