Unser Data Scientist Dr. Michael Kenning erklärt die Intuitionen, die graphenbasierte Faltungen und graphenbasierte Convolutional Neural Networks ermöglicht haben.
Die Arbeit mit Daten erfordert weitreichende Annahmen über deren Struktur. Bei einer Zeitreihe gehen wir im Allgemeinen davon aus, dass jeder Datenpunkt in einem festen zeitlichen Abstand zum vorherigen und zum nächsten Messwert steht. Ein Pixelraster in einem Bild besitzt – unabhängig von der Auflösung – eine feste Struktur: Jedes Pixel hat Nachbarn oben, unten, links und rechts. Mit anderen Worten: Wir treffen eine Annahme über die Regelmäßigkeit der Daten.
Es überrascht nicht, dass die von uns entwickelten Algorithmen Regelmäßigkeit voraussetzen. Doch die reale Welt ist selten so geordnet wie ein Pixelraster oder die gleichmäßigen zeitlichen Abstände einer Zeitreihe. Tatsächlich wird Regularität oft aufgezwungen – selbst dort, wo sie von Natur aus nicht vorhanden ist.
Was also tun mit unregelmäßigen Strukturen? Die Mathematik hält glücklicherweise eine ganze Reihe von Lösungen bereit – eine davon ist der Graph. Graphen sind ein klassisches Konzept mit langer Geschichte, wurden jedoch erst vergleichsweise spät in der Entwicklung neuronaler Netze eingesetzt.
Nachdem das Convolutional Neural Network (CNN, faltendes neuronales Netz) im Jahr 2012 bei einem Bildklassifizierungswettbewerb seine Konkurrenten deutlich übertroffen hatte, erlangte es große Bekanntheit und leitete eine Welle von Fortschritten in der Bildverarbeitung und anderen etablierten Anwendungsbereichen ein. Naheliegend war daher die Frage, ob sich dieses Modell auch auf Graphen anwenden ließe. Tatsächlich entwickelte sich der Graph rasch zum Eckpfeiler eines eigenen Forschungszweigs innerhalb des Deep Learning: dem Graph Deep Learning, das sich mit graphenstrukturierten Daten befasst.
In diesem Blogbeitrag zeige ich die grundlegenden Ideen auf, die graphbasierte Faltungen und sogenannte Graph Convolutional Neural Networks (GCNs) ermöglichen. Am Ende werden Leser ein gutes Verständnis sowohl der Vorteile von Graphen in der Computermodellierung als auch der praktischen Herausforderungen bei ihrer Anwendung gewonnen haben. Der Beitrag ist wie folgt aufgebaut:
- Beispiele für unregelmäßige Strukturen — Im ersten Abschnitt skizziere ich einige alltägliche Beispiele, in denen unregelmäßige Strukturen vorherrschen.
- Was ist ein Graph? — Eine kurze Einführung in den Graphenbegriff und die Terminologie, die in den folgenden Abschnitten hilfreich ist.
- Wie können Graphen verwendet werden? — Anhand eines Beispiels mit Fabriksensoren erkläre ich, wie Graphen eingesetzt werden können.
- Von der Faltung auf Bildern zur Faltung auf Graphen — Die grundlegenden Intuitionen der Faltung auf Bildern und Rastern werden vorgestellt und anschließend deren Übertragbarkeit auf Graphen erläutert.
- Schließlich, räumliche Faltung und spektrale Faltung auf Graphen — Diese theoretisch anspruchsvollsten Abschnitte helfen dabei, die Herausforderungen bei der Definition von Faltungen auf Graphen zu verstehen.
Beispiele für unregelmäßige Strukturen
Viele Netzwerke haben keine regelmäßige Struktur. Um beispielsweise einen Fehler in einem Computernetzwerk zu finden, müssen wir das Problem durch das Netzwerk verfolgen können – das heißt: Wir müssen wissen, wie die Maschinen miteinander verbunden sind. Ein fehlerhafter Switch kann – je nach seiner Position im System – den Ausfall von zehn, hundert oder sogar mehr Computern verursachen.
Ein anderes Beispiel: Stellen wir uns eine große Fabrik mit zwei Einheiten vor, Einheit 1 und Einheit 2, von denen jede Hunderte von Sensoren besitzt. Um herauszufinden, was in Einheit 1 passiert, würden wir nicht die Sensoren von Einheit 2 betrachten. Innerhalb einer Einheit dagegen erwarten wir – in unterschiedlichem Maße – Korrelationen zwischen den Sensoren. Ein Temperaturwert könnte den Druck stärker beeinflussen als das Eingangsvolumen. Umgekehrt kann das Eingangsvolumen zu einem Zeitpunkt die Temperatur im nächsten besser vorhersagen als etwa der elektrische Eingang.
Mit anderen Worten: Nicht jeder Sensor steht in gleicher Beziehung zu allen anderen. Es wäre hilfreich, solche Beziehungen abbilden zu können – und genau das ermöglichen Graphen.
Was ist ein Graph?
Ein Graph ist ein erfreulich einfaches mathematisches Objekt: Er besteht aus Knoten (engl. vertices) und Kanten (engl. edges). Zwischen jedem Knotenpaar kann entweder eine Verbindung bestehen – oder eben nicht. Sind zwei Knoten durch eine Kante verbunden, nennt man sie benachbarte Knoten.
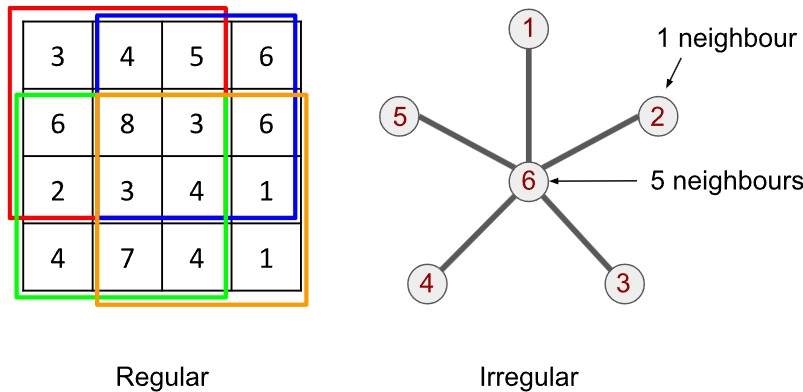
Ein klassisches Beispiel ist der sogenannte Sterngraph, der unten dargestellt ist: Ein zentraler Knoten (hier mit der Zahl 6 bezeichnet) ist mit fünf anderen Knoten (1 bis 5) verbunden. Man sagt: Knoten 6 hat den Grad 5, da er fünf Verbindungen besitzt. Die übrigen Knoten haben jeweils den Grad 1. Jeder Knoten hat also eine bestimmte Anzahl von Nachbarn – entweder einen oder fünf.
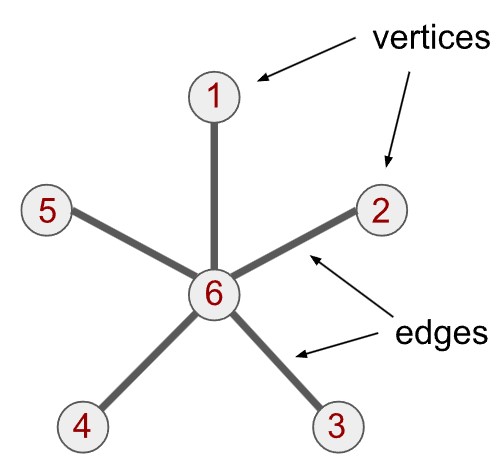
Knoten können viele Dinge repräsentieren, werden jedoch häufig verwendet, um Variablen oder Datenquellen darzustellen. Die Kanten beschreiben dabei, wie diese Variablen miteinander in Beziehung stehen. Wenn die Knoten zum Beispiel Computer repräsentieren, könnten die Kanten ausdrücken, welche Rechner physisch miteinander verbunden sind. Der gesamte Graph würde in diesem Fall die Struktur eines Computernetzwerks abbilden.
Der oben gezeigte Graph wird als einfacher Graph bezeichnet. Es gibt jedoch zahlreiche Variationen, mit denen sich unterschiedliche Arten von Beziehungen modellieren lassen. Eine davon ist der gerichtete Graph, bei dem jede Kante eine Richtung hat. Betrachten wir dazu folgendes Beispiel:
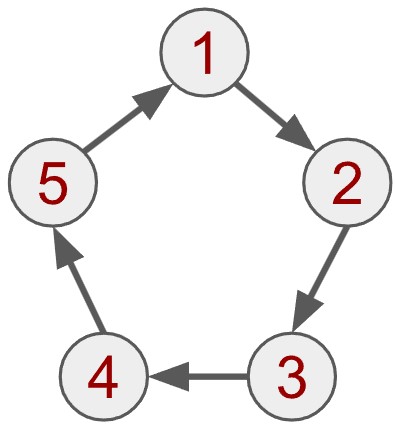
In einem gerichteten Graphen gilt eine Beziehung nur in eine Richtung. Man kann sich das wie Wasser vorstellen, das durch ein geschlossenes System gepumpt wird – es fließt von Knoten 1 zu Knoten 2, aber nicht zurück (oder zumindest sollte es das nicht).
Solche gerichteten Verbindungen können beispielsweise unidirektionale Abhängigkeiten darstellen: Wenn eine wissenschaftliche Arbeit 1 die Arbeit 2 zitiert, heißt das nicht, dass auch Arbeit 2 Arbeit 1 zitiert. Der Graph kann in diesem Fall als ein Kreis von Zitaten interpretiert werden – jede Arbeit verweist auf die nächste, aber nicht zurück.
Ein Graph kann zudem Knoten mit sehr unterschiedlichen Graden enthalten. Nichts hindert uns daran, einen Sterngraphen mit hundert Knoten zu zeichnen, in dem ein einziger zentraler Knoten mit allen anderen verbunden ist.
Wie Graphen für Fabriksensoren verwendet werden können
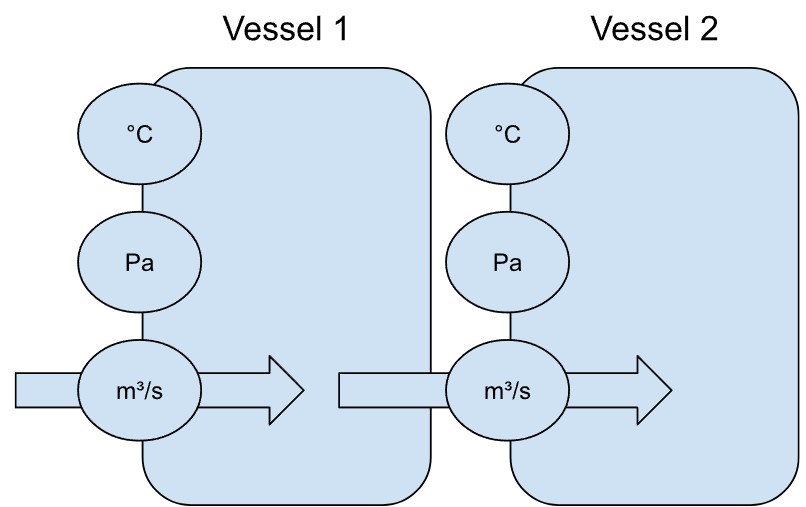
Kehren wir zum Beispiel mit den Sensoren zurück: Stellen wir uns mehrere Sensoren vor, die die Bedingungen in einem beheizten Behälter in einer Fabrik erfassen – nennen wir ihn Behälter 1 (engl. vessel 1). Steigt allein die Temperatur, erwarten wir auch einen Anstieg des Drucks. Ebenso würde eine Erhöhung der Zufuhrrate den Druck beeinflussen.
Diese wechselseitigen Abhängigkeiten zwischen den Sensoren lassen sich in Form eines Graphen modellieren – wobei die Knoten die Sensoren darstellen und die gerichteten Kanten die vermuteten Einflussrichtungen.
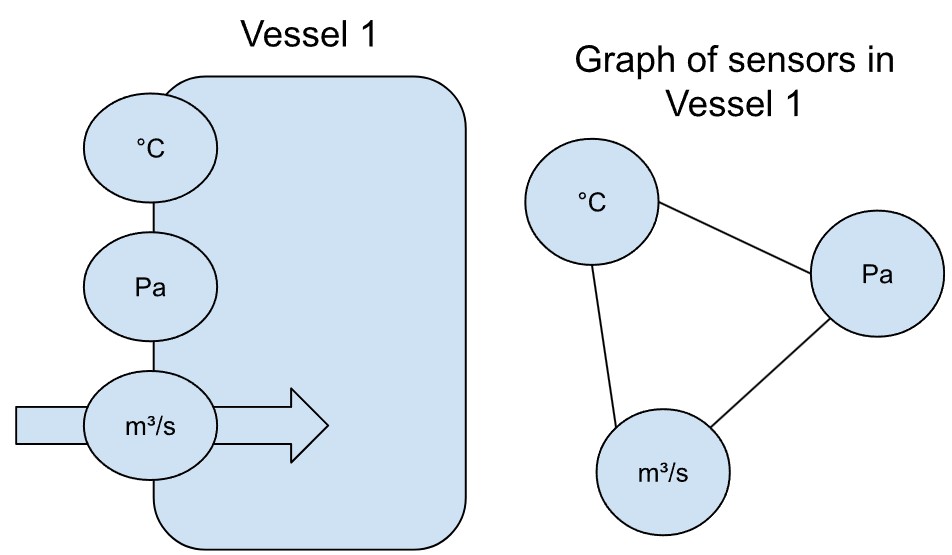
Angenommen, es gibt einen zweiten, identischen Behälter (vessel 2, siehe unten) mit denselben Sensoren. Dann würden wir auch hier ähnliche Wechselwirkungen zwischen Temperatur, Druck und Zufuhrrate erwarten.
Solange die beiden Behälter nicht miteinander verbunden sind, beeinflussen sich ihre Messwerte gegenseitig nicht. Die Sensoren beider Behälter ließen sich daher mit derselben grundlegenden Graphenstruktur modellieren – allerdings nicht mit exakt identischen Graphen.
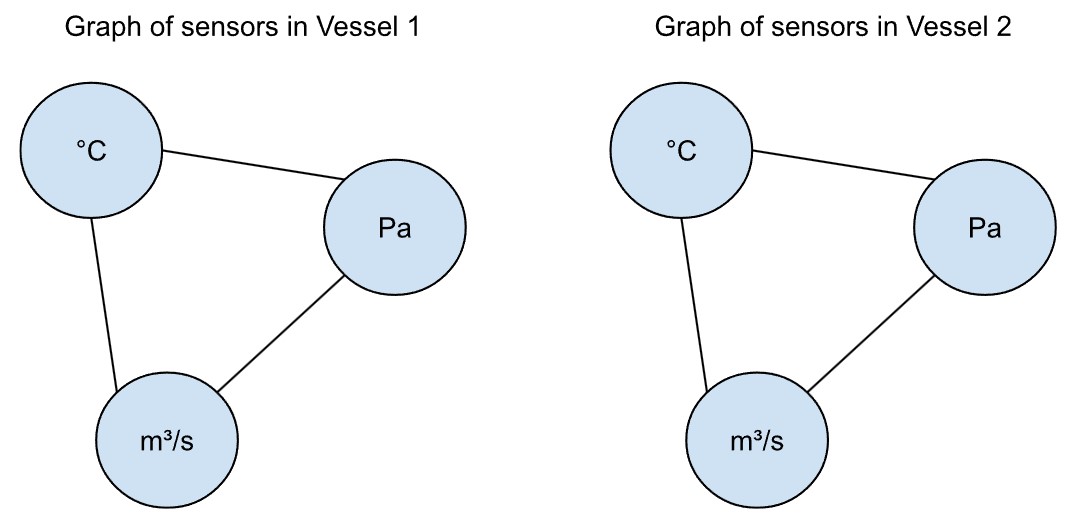
Wenn der Output von Behälter 1 (vessel 1) als Input für Behälter 2 (vessel 2) dient, ist es sehr wahrscheinlich, dass die Bedingungen in Behälter 1 auch Behälter 2 beeinflussen.
In diesem Fall lassen sich die beiden Behälter durch einen gerichteten Graphen darstellen.
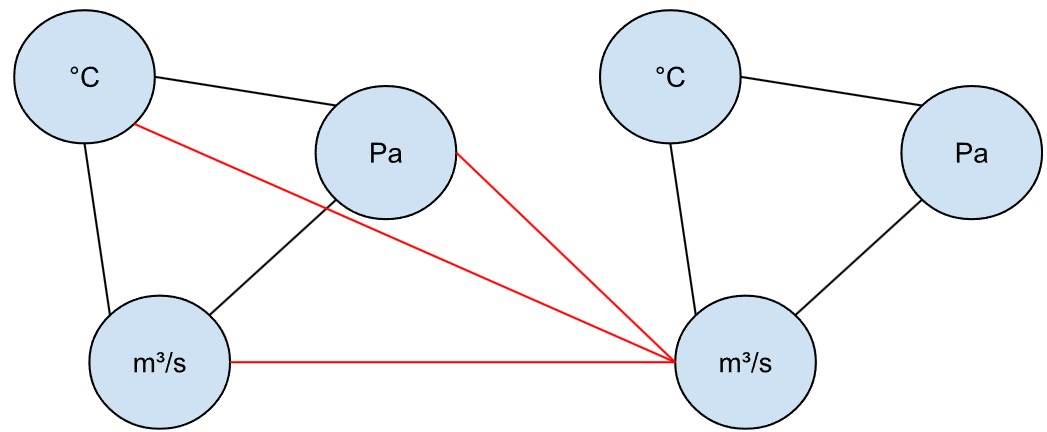
Tatsächlich könnten wir die Behälter sogar als gerichteten Graphen darstellen, bei dem die Sensoren von Behälter 1 mit dem Input von Behälter 2 verbunden sind – jedoch nicht umgekehrt.
Von der Faltung auf Bildern zur Faltung auf Graphen
Bisher haben wir Graphen vor allem als nützliches Werkzeug genutzt, um visuell darzustellen, wie Sensoren miteinander verbunden sind. Glücklicherweise wurden in den letzten Jahren zahlreiche Techniken entwickelt, die mithilfe von Graphstrukturen lernen können. Diese Methoden basieren auf Convolutional Neural Networks (CNNs), die sonst hauptsächlich bei Bildern zum Einsatz kommen. Wenn wir bestimmte Einschränkungen aufheben, lassen sich CNNs auch auf Graphen anwenden.
In diesem Abschnitt werden wir anhand einiger Analogien zwischen Bildern bzw. Rastern und Graphen nachvollziehen, wie das möglich ist.
Auf einem Graphen strukturierte Signale
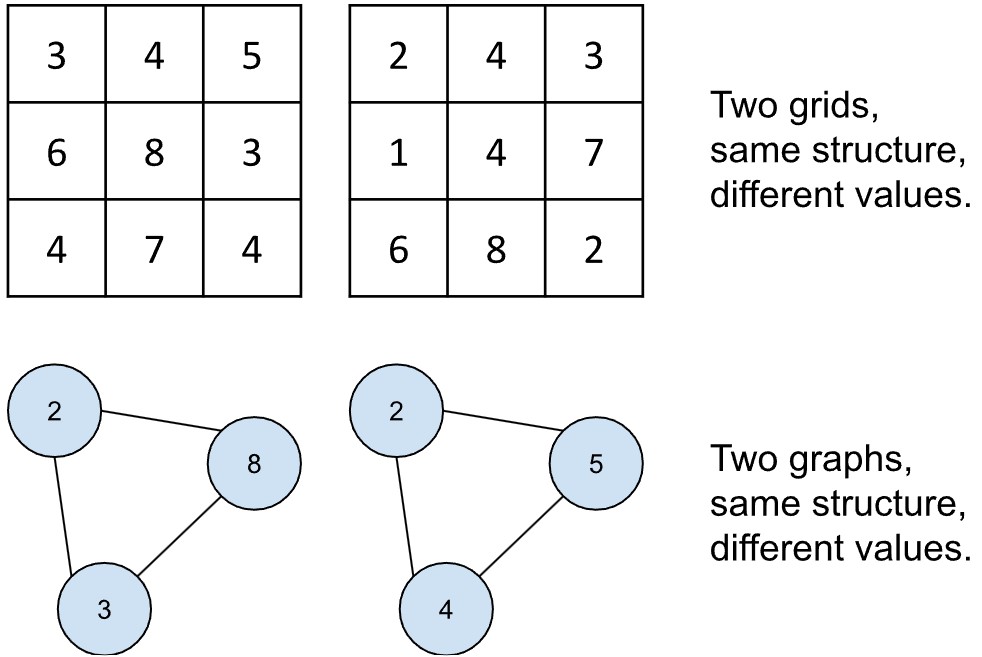
Man kann Graphen gut mit Bildern vergleichen. Was ist ein Bild? Es ist ein Raster aus Werten. Wenn zwei Bilder dieselbe Größe haben, liegt das daran, dass sie dieselben Dimensionen besitzen: Zum Beispiel 86 Spalten und 86 Zeilen.
Doch obwohl zwei Bilder die gleiche Struktur haben, müssen ihre Werte nicht identisch sein. Die einzelnen Rasterzellen sind sozusagen Platzhalter, die beliebige Zahlen annehmen können. Mit anderen Worten: Sie teilen eine gemeinsame Struktur, unterscheiden sich jedoch im Inhalt – dem sogenannten Signal.
Dieses Prinzip lässt sich leicht auf das Beispiel mit den Behältern übertragen. In der vorherigen Abbildung haben wir die Graphstruktur beschrieben. Zu einem bestimmten Zeitpunkt melden die Sensoren bestimmte Messwerte, zu einem anderen Zeitpunkt andere. Die Struktur des Graphen bleibt dabei unverändert, nur die Signale ändern sich. Wenn wir diese Messwerte im Kontext des Graphen betrachten, sprechen wir von Graphensignalen.
Die Möglichkeit, Signale präziser in Form von Graphen zu strukturieren, hat zur Entstehung eines neuen Forschungsfeldes geführt: dem Graph Deep Learning. Dieses baut auf Arbeiten aus den 1990er- und 2000er-Jahren auf und verknüpft sie mit den Prinzipien von Convolutional Neural Networks (CNNs).
Im nächsten Schritt werden wir zunächst die Faltung (Convolution) erläutern, bevor wir zeigen, wie sie auf Graphen angewendet werden kann.
Wie Faltung auf regulären Domänen auf Graphen funktionieren kann
Convolutional Neural Networks, deren Kernoperation die Faltung ist, wurden ursprünglich in den 1990er Jahren auf Bilder von Ziffern angewendet.
Ein Bild ist im Grunde ein Raster – eine Matrix aus Pixeln – und damit eine regelmäßige Struktur. Genau diese regelmäßige Struktur setzt die Faltung voraus.
Dabei wird ein kleines, quadratisches Gitter von Werten, der sogenannte Kernel oder Filter, über das Bild “geschoben” und an jeder Position mit dem entsprechenden Teil des Bildes multipliziert. (Man kann sich den Kernel wie einen Plätzchenausstecher vorstellen, der Formen aus dem Bild “aussticht”.)
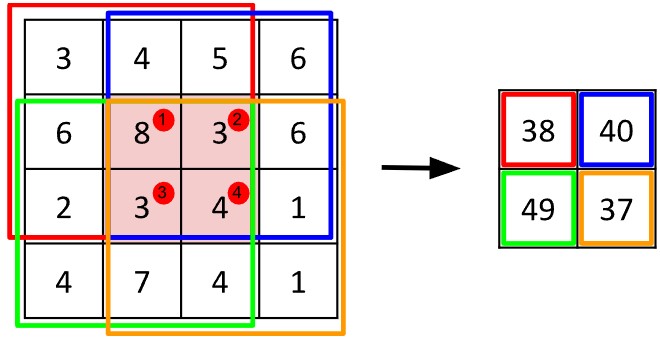
Abb. 8: Ein Beispiel für eine Faltung: Jeder farbige 3x3-Quadrat-Kernel führt dieselbe Operation aus – er summiert die Werte in seinem Bereich. Jede Farbe steht dabei für denselben Kernel an einer anderen Position, jeweils zentriert auf einem der vier rot markierten Pixel.
Die Werte in den roten Kreisen geben die Reihenfolge der Faltung an: von links nach rechts und von oben nach unten. Aufgrund von Randbedingungen fällt die Ausgabe etwas kleiner aus als das Eingabebild.
In diesem Beispiel besteht der Kernel aus einem 3x3-Gitter mit Einsen. Die Operation auf Zelle 1 sieht folgendermaßen aus:
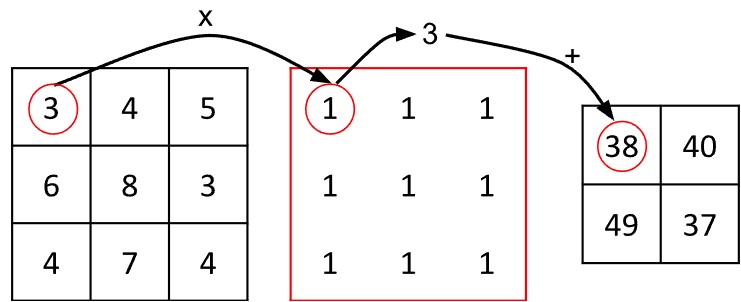
Betrachten wir den Algorithmus genauer: Der Kernel ist 3×3 Einheiten groß, ebenso wie jeder Bildausschnitt, auf den er angewendet wird. Man kann sich diesen Bildausschnitt als ein zentrales Pixel mit acht Nachbarn vorstellen.
Wenn der Kernel auf den Bildausschnitt gelegt wird, liegt jeder Wert des Kernels genau über einem Pixel. Im nächsten Schritt werden die Werte des Kernels elementweise mit den darunterliegenden Pixelwerten multipliziert – eine Operation, die als Hadamard-Produkt bezeichnet wird.
Die resultierenden Werte werden anschließend aufsummiert, wodurch ein neuer Wert für das zentrale Pixel entsteht.
Der Algorithmus arbeitet systematisch und nicht willkürlich: Die Faltung erfolgt von links nach rechts und von oben nach unten über das gesamte Bild. Das Ergebnis jeder Faltung wird an der entsprechenden Position in einer neuen Ausgabematrix gespeichert.
Die Ausgabematrix kann kleiner sein als die ursprüngliche Eingabematrix – warum? An den Rändern des Bildes fehlen Nachbarn. Entweder überspringen wir diese Randpixel komplett, wodurch die Ausgabematrix schrumpft, oder wir nehmen an, dass außerhalb des Bildes Nullen stehen, was als Zero-Padding bezeichnet wird. Unabhängig von der Methode müssen solche Randbedingungen berücksichtigt werden.
Ein Kernel kann beliebige Werte enthalten, zum Beispiel solche, die Linien im Bild erkennen. Sobald diese Linien erkannt sind, können sie in weiteren Schritten zu größeren Formen wie Kreisen und schließlich zu komplexeren Objekten wie Gesichtern zusammengesetzt werden. Dieses Prinzip – kleine Merkmale zu größeren, abstrakten Strukturen zu kombinieren – verleiht Convolutional Neural Networks ihre enorme Leistungsfähigkeit, da praktisch alle auf der Faltung basieren.
Eine Faltung in dieser Form setzt jedoch eine regelmäßige Gitterstruktur voraus. Graphen haben keine solche Regelmäßigkeit: Anders als bei Bildern können Knoten eines Graphen eine beliebige Anzahl von Nachbarn besitzen, und es ist nicht möglich, einen Kernel einfach über die Oberfläche eines Graphen “zu schieben”.
Wie kann man Faltungen auf Graphen anwenden? Wie kann ein Computer aus einem Gebilde, das im Wesentlichen aus Punkten und Linien besteht, sinnvolle Informationen gewinnen? Es erfordert etwas Trickserei, aber es ist möglich. Dabei gibt es zwei Hauptansätze: die räumliche Graphenfaltung und die spektrale Graphenfaltung.
Räumliche Faltung auf Graphen
Die räumliche Faltung auf Graphen ähnelt der Faltung auf Bildern sehr stark. Der Algorithmus ist dabei recht einfach:
Stellen wir uns vor, wir verwenden denselben Kernel wie zuvor – einen, der die Werte aller Nachbarn einer zentralen Zelle aufsummiert. Statt einer zentralen Zelle gibt es nun einen zentralen Knoten. Wie jedes Pixel im Bild eine Reihe von Nachbarn hat, besitzt auch jeder Knoten im Graphen eine Menge von Nachbarn.
Die Faltung auf Graphen funktioniert daher konzeptionell ähnlich. Schauen wir uns den Prozess in drei Schritten veranschaulicht an:
- Daten auf dem Graphen strukturieren: Die Werte an jedem Knoten bilden das Signal für diesen Knoten.
- Nachbarsignale sammeln und aggregieren: Für jeden Knoten suchen wir alle seine Nachbarn, sammeln deren Signale und summieren sie auf.
- Wert zuweisen: Den so berechneten aggregierten Wert weisen wir dem jeweiligen zentralen Knoten neu zu.
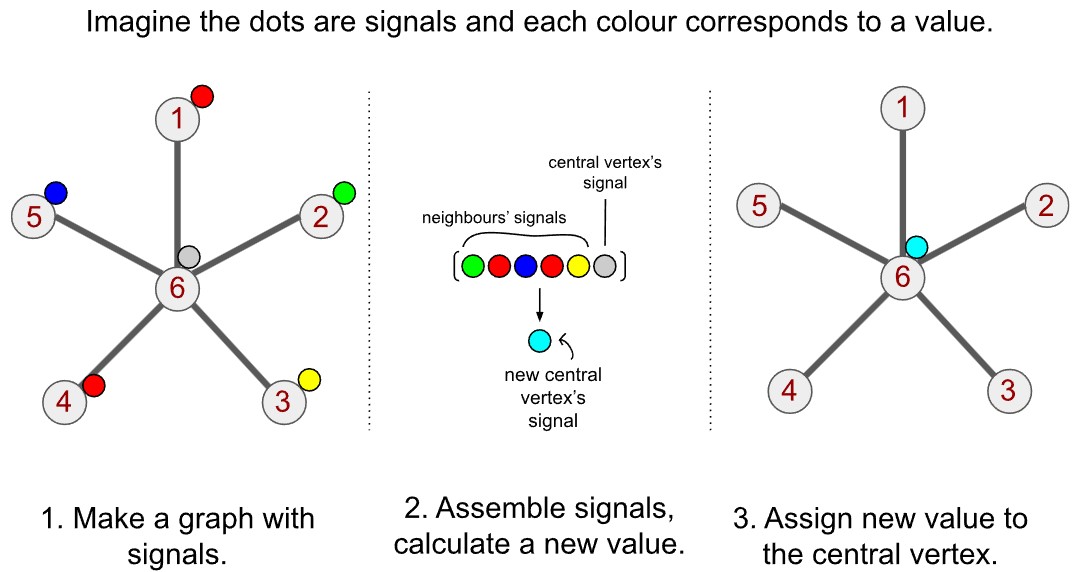
Im obigen Beispiel mit dem Kernel aus Einsen entspricht die Faltung im Grunde einer einfachen Summe der Werte. Auch bei Graphen kann Schritt 2 als Summation betrachtet werden.
Doch grundsätzlich ist die Definition der Operation auf den Nachbarwerten sehr flexibel: Man könnte eine gewichtete Summe berechnen, das Produkt der Werte bilden, ein einzelnes Signal auswählen und die anderen ignorieren oder eine Teilmenge der Signale für eine bestimmte Operation verwenden.
Die Art und Weise, wie man die Faltung definiert, kann also je nach Anwendung stark variieren.
Das Problem der Ordnungslosigkeit in Graphen
Diese Flexibilität hat jedoch ihren Preis. Erinnern wir uns an das Beispiel mit dem 3×3-Gitter-Kernel: Es hat immer dieselbe Größe und kann überall im Bild angewendet werden. Zudem erwarten wir, dass an jeder Position im Kernel die Werte eine feste räumliche Bedeutung haben – also links, rechts, oben, unten relativ zum zentralen Pixel. Diese Regularitätsannahme erlaubt es uns, Positionen im Kernel eindeutig mit Richtungen zu verknüpfen.
Das ist entscheidend, um beispielsweise vertikale von horizontalen Linien unterscheiden zu können.
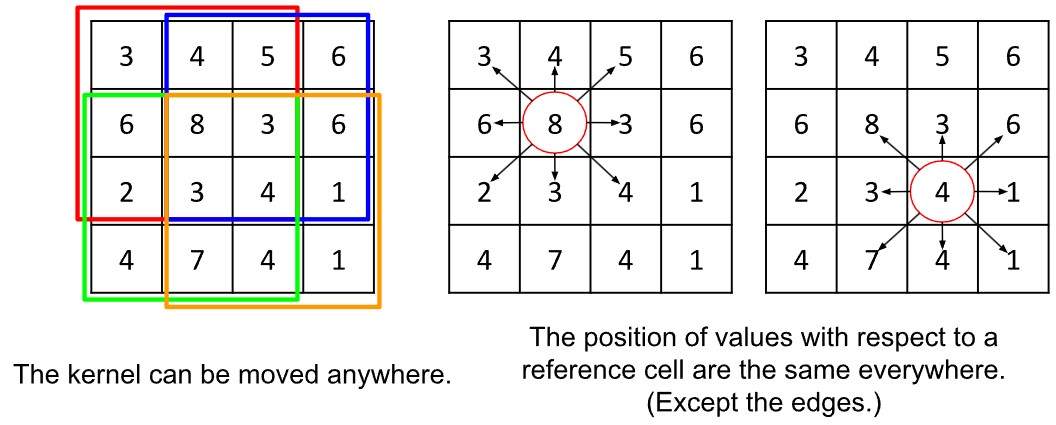
Links: Der Filter kann sich überall hinbewegen.
Rechts: Die Position der Werte bezogen auf eine Referenzzelle sind überall die gleichen (außer an den Rändern).
Das Gleiche gilt jedoch nicht für Graphen. Jeder Knoten kann eine unterschiedliche Anzahl von Nachbarn haben, weshalb wir keine feste Anzahl von Gewichten definieren können, die wir auf die Nachbarn anwenden. Zudem gibt es keine Möglichkeit, die Nachbarn an feste Positionen zu binden: Begriffe wie “oben”, “unten”, “links” oder “rechts” existieren im Graphen nicht. Knoten sind entweder verbunden oder nicht, sie besitzen keine kardinale Position – was jedoch den Vorteil mit sich bringt, dass keine Randbedingungen nötig sind.
Es gibt verschiedene Ansätze, um mit dem Fehlen einer kardinalen Position umzugehen. Eine Lösung besteht darin, wie beim klassischen Kernel einen festen Satz von Gewichten festzulegen. Angenommen, in einem gegebenen Graphen hat jeder Knoten mindestens drei Nachbarn. Dann definiert man eine Liste von vier Gewichten – eines davon für den zentralen Knoten. Für jeden Knoten summiert man die Signale seiner Nachbarn entsprechend der Gewichtung.
Multiplizieren wir das Signal des zentralen Knotens mit dem ersten Gewicht und die Signale der Nachbarn mit den übrigen drei Gewichten. Welche Nachbarn welchem Gewicht zugeordnet werden, lässt sich auf verschiedene Arten lösen – insbesondere, wenn umfangreiches Domänenwissen vorliegt. Manchmal gibt die Domäne sogar eine natürliche, kardinale Ordnung der Knoten vor.
Für eine vertiefte Diskussion dieser theoretischen Fragestellungen empfehle ich die Studie, die ich während meiner Promotion an der Swansea University mitverfasst habe.
Spektrale Faltung auf Graphen
Die spektrale Faltung ist mathematisch komplexer, weshalb ich hier auf detaillierte Erklärungen verzichte.
Um die graphenstrukturierte Information in ihr Spektrum zu transformieren, benötigen wir eine matrixähnliche Basis, auf der diese Umwandlung erfolgen kann. Glücklicherweise lassen sich Graphen als Matrizen darstellen.
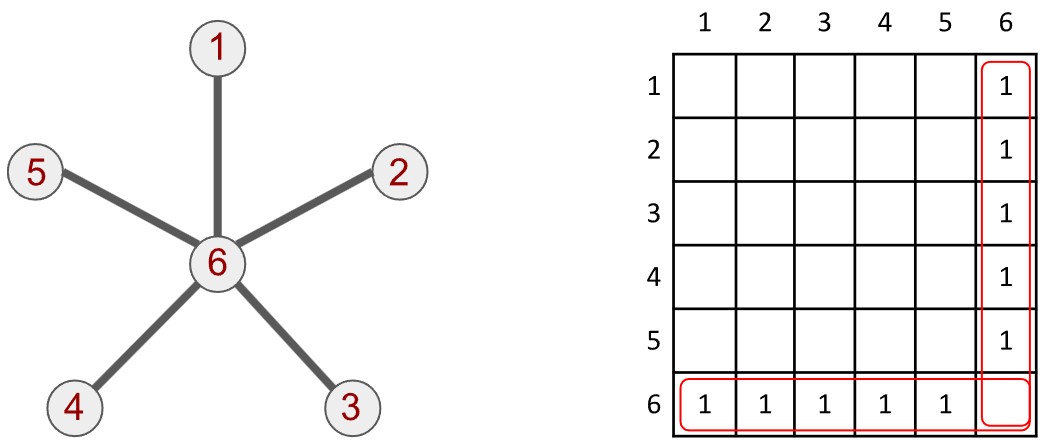
Der Graph wird einem Computer üblicherweise als binäre Matrix dargestellt – eine Matrix, deren Einträge 1 oder 0 sind. Der oben gezeigte Sterngraph wird durch die danebenstehende Matrix beschrieben (obwohl wir nur die Einsen eintragen, sind die Nullen natürlich implizit vorhanden). Diese Matrix nennt man Adjazenzmatrix, weil jede Zeile und Spalte jeweils einem bestimmten Knoten zugeordnet ist und beschreibt, welche Knoten im Graphen benachbart sind.
Sowohl die Zeile als auch die Spalte, die mit Knoten 6 verknüpft sind, enthalten viele Einsen – mit Ausnahme der Zelle auf der Diagonalen (die sechste Zelle), wie hervorgehoben. Umgekehrt haben die Zeilen und Spalten für die anderen Knoten jeweils nur eine Eins in der Spalte beziehungsweise Zeile, die Knoten 6 entspricht.
Die Adjazenzmatrix ist für die spektrale Graphenfaltung essenziell. Sie ermöglicht die Berechnung der Laplace-Matrix, mit deren Hilfe wir die räumliche Information in die entsprechende spektrale Information transformieren können. Das ist vergleichbar damit, wie man die Frequenzzusammensetzung eines Sprachsignals auf einem Monitor visualisiert, wenn man in ein Mikrofon spricht. Sobald diese Transformation erfolgt ist, können wir Filter auf das Spektrum des Graphen anwenden – was definitionsgemäß einer Faltung entspricht.
Einige weitere Ideen zur Verwendung von Graphen
In diesem Blogbeitrag habe ich die Intuitionen hinter Graphen und der Graphenfaltung erläutert. Ausgehend von einem konkreten Beispiel – Sensoren in einer Fabrik – wurde gezeigt, wie Graphen vielfältig einsetzbar sind. Netzwerke ganz unterschiedlicher Art (Computernetzwerke, soziale Netzwerke, Verkehrsnetze) sind meist höchst unregelmäßig strukturiert. Andere Anwendungsbereiche mögen den Leser überraschen: Elektroden eines Elektroenzephalogramms, Interaktionen in Multi-Agenten-Systemen, Molekülchemie oder Krankheitsmodelle – alles, was es braucht, ist eine passende Formulierung des jeweiligen Problems.
Letztendlich sind Graphen sowohl bei der Problemformulierung als auch bei der Analyse von Daten äußerst nützlich. Sie sind intuitive und einfache mathematische Objekte mit großer Erklärungskraft. Das Konzept des Graphen ermöglicht es, Techniken, die für reguläre Domänen entwickelt wurden, auch auf unregelmäßige Strukturen anzuwenden.
Weiterführendes Lesematerial zu Graphen
Einige Arbeiten werden häufig zitiert und sind nach wie vor relevant, wenn Sie mehr über die Anwendungen von Deep Learning auf Graphen und andere unregelmäßige Strukturen erfahren möchten.
- D. I. Shuman, S. K. Narang, P. Frossard, A. Ortega and P. Vandergheynst, “The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains,” in IEEE Signal Processing Magazine, vol. 30, no. 3, pp. 83-98, May 2013.
- M. M. Bronstein, J. Bruna, Y. LeCun, A. Szlam and P. Vandergheynst, “Geometric Deep Learning: Going beyond Euclidean data,” in IEEE Signal Processing Magazine, vol. 34, no. 4, pp. 18-42, July 2017.
- Hamilton, Ying, und Leskovec, “Representation Learning on Graphs: Methods and Applications”, arXiv preprint arXiv:1709.05584 (2017).
Falls Sie einen umfassenden Überblick über die Theorie und die Herausforderungen des Graph Deep Learning suchen, den ich vor einigen Jahren gemeinsam mit einem Kollegen an der Swansea University verfasst habe, lade ich Sie herzlich ein, unsere öffentlich zugängliche Übersichtsarbeit zu lesen.
Wenn Sie sich allgemein für Deep Learning und Convolutional Neural Networks interessieren, könnten die folgenden Bücher und Artikel für Sie spannend sein:
- LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
- Goodfellow, Bengio, und Courville, Deep Learning, 2016.
Abschließend sei zum Thema Graphentheorie ein maßgeblicher Text von Béla Bollobás empfohlen. Das einführende Buch, insbesondere das erste Kapitel, bietet eine solide Grundlage.
Über den Autor:

Dr. Michael Kenning promovierte 2023 in Informatik an der Swansea University in Wales. Seine Forschung fokussierte sich auf die Anwendung von Deep-Learning-Methoden auf graphenstrukturierte Daten. Dabei untersuchte er insbesondere Techniken, mit denen die Struktur der Graphen selbst direkt aus den Daten erlernt werden kann. In seiner Freizeit liest er gern und widmet sich dem Sprachenlernen.