Initially, large language models like ChatGPT were known for their weaknesses in mathematics – today, they solve complex competition-level problems. This article explores the rapid advances of AI in the field of mathematics.
Why are LLMs so bad at math?
At least until 2023, Large Language Models (LLMs) like ChatGPT or LLaMA were of little help with mathematical tasks. While the answers often sounded fluent and coherent, the reasoning was frequently flawed – or the calculations simply wrong. Here are two example questions from the Cognitive Reflection Test by S. Frederick [1].
Question 1: If it takes five machines five minutes to make five widgets, how long would it take 100 machines to make 100 widgets?
An intuitive but incorrect answer might be "100 minutes". The following solution is also wrong.
Answer from LLaMA-2-13B [2]:
If it takes five machines five minutes to make five widgets, that means each machine takes one minute to make one widget. With 100 machines, each machine will take one minute to make one widget. So, it will take all 100 machines one minute to make 100 widgets.
However, the correct answer is "5 minutes".
Question 2: In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?
Answer from LLaMA-2-13B:
This is a classic example of exponential growth. On day 48, the patch of lily pads covers the entire lake. To find out how long it would take for the patch to cover half of the lake, we can use the fact that the patch doubles in size every day. So, if it takes 48 days to cover the entire lake, it would take half that time (or 48 / 2 = 24 days) to cover half of the lake.
Although the LLM correctly identifies "exponential growth", it fails to calculate the correct solution, which is not 24, but 48 − 1 = 47 days.
The failure of LLMs on simple math problems may seem surprising at first – after all, it's a computer program failing at calculations. However, the computations performed by an LLM follow the internal logic of the underlying neural network and are therefore sometimes nonsensical with respect to the semantics humans would expect.
In this regard, an LLM’s responses can be better understood using a model by psychologist Daniel Kahneman. Kahneman distinguishes between two systems of human thought. System 1 is intuitive, automatic, and fast. It operates associatively and uses learned patterns, such as recognizing faces or completing sentences. The heuristics of System 1 are extremely valuable, as they draw on our experience and learned knowledge. On the other hand, System 1 is prone to numerous biases and misjudgments. (Recommended reading: Kahneman’s book Thinking, Fast and Slow.)
For small calculations like 2+3, System 1 is sufficient, at least for adults who have memorized the answer. When a child tries to calculate 2 + 3, or an adult attempts to solve 19 × 57 mentally, System 2 is engaged. This system works analytically, logically, and requires more time and energy. We use it for reasoning, deliberation, and solving complex problems.
An LLM can be understood as a System 1: a pattern matcher that has learned an enormous number of associations. Its responses may appear fluent and convincing, but they are primarily too impulsive for more complex analytical thinking. In mathematics, where logical precision is essential, this weakness becomes particularly apparent.
What is 19 × 57?
System 2 answer: With maximum concentration, we calculate 19 × 57 = 10 × 57 + 9 × 57 = 570 + 513 = 1083.
System 1 answer: An estimate for 19 × 57 might be something like 19 × 57 ≈ 20 × 50 = 1000. However, if the calculation is familiar or has been practiced frequently, a System 1 response might retrieve the correct answer 1083 automatically.
Why are LLMs so good at math?
Meanwhile, LLMs are performing significantly better on mathematical tasks, as illustrated by the turquoise line (Competition-level mathematics (MATH)) in the following graphic from the AI Index 2025 Annual Report [3].
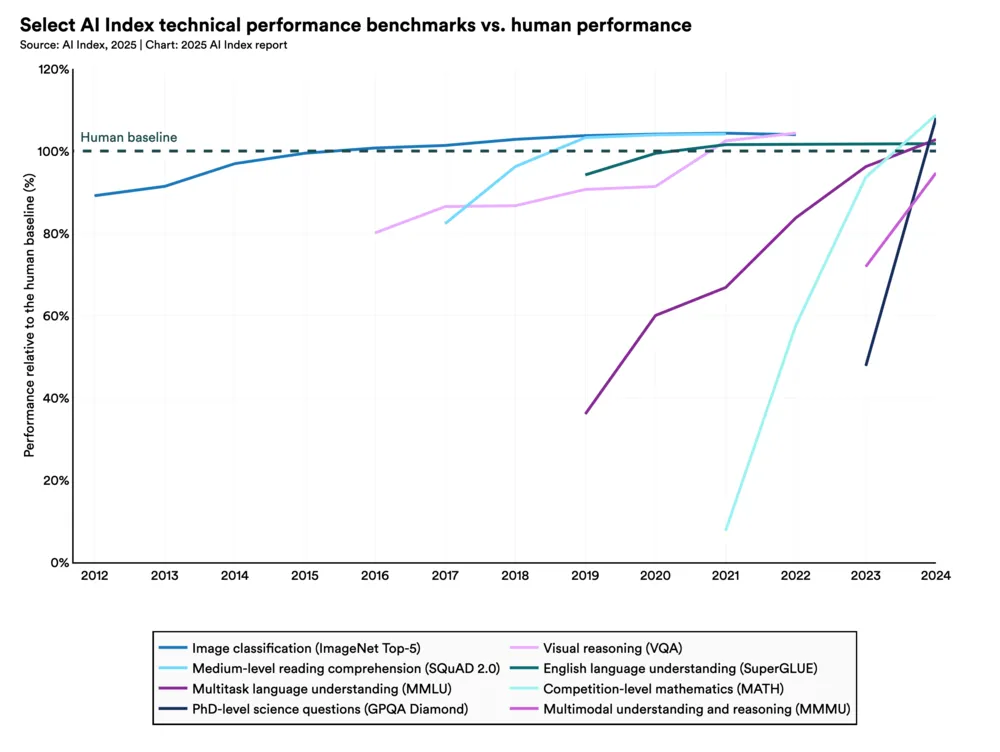
Chart from the The AI Index 2025 Annual Report, used under the license CC BY-ND 4.0.
The mathematics benchmark consists of problems from school competitions [4], for example:
Problem: Tom has one red marble, one green marble, one blue marble, and three identical yellow marbles. How many different groups of two marbles can Tom choose?
Solution: There are two cases: Either Tom chooses two yellow marbles (1 outcome), or he chooses two marbles of different colors ( outcomes). The total number of different pairs of marbles Tom can choose is .
The rapid improvement of LLMs in mathematical performance can be attributed at least to the following two approaches:
- External System 2: Since LLMs excel at linguistic pattern recognition, they can at least identify when a mathematical question is being asked. Such queries can then be forwarded to external tools – like a calculator, a computer algebra system, a Python program, or similar. In this case, System 1 effectively seeks assistance from an external System 2. (Currently, the open-source framework Model Context Protocol by the company Anthropic appears to be gaining traction for this kind of interaction between LLMs and external data sources.)
- Emulated System 2: Another concept that helps LLMs engage in more deliberation and analytical thinking is Chain-of-Thought Prompting. By guiding the LLM to respond step-by-step and to question its own intermediate results through feedback loops, it can act much more reflectively and better grasp complex problems. In a way, this technique simulates a System 2.
Question: Tom has one red, two identical green, three identical yellow, and three identical blue marbles. How many different groups of three can Tom choose?
ChatGPT (o4-mini) provides its thought process for finding the solution, in addition to the final answer:
I will think about how many ways there are to choose 3 balls from the given colors (red, green, yellow, blue) considering the limits on the colors. I will approach this with a calculation that can be solved either manually or by a small program to find the number of groups and thus the answer.
It then writes a Python program that delivers the correct solution, 15, through iteration:
count = 0
triples = []
for r in range(0,2):
for g in range(0,3):
for y in range(0,4):
for b in range(0,4):
if r+g+y+b == 3:
count += 1
triples.append((r, g, y, b))
count, triples[:10]
Output:
(15, [(0, 0, 0, 3), (0, 0, 1, 2), (0, 0, 2, 1), (0, 0, 3, 0),
(0, 1, 0, 2), (0, 1, 1, 1), (0, 1, 2, 0), (0, 2, 0, 1),
(0, 2, 1, 0), (1, 0, 0, 2)])
The digitization of mathematics
An LLM acquires its mathematical knowledge in much the same way humans do – through books, lecture notes, scientific articles, forum posts, and so on. However, mathematical knowledge could fundamentally be represented in a different way – digitally and independently of human language. The theoretical foundations of computer science historically emerged from fundamental questions in mathematics and logic. Ironically, mathematics itself has so far been only sporadically or not at all digitized.
Although several so-called formal languages have been developed for this very purpose over the past 100 years – essentially programming languages for mathematics – mathematical knowledge, i.e., definitions, conjectures, theorems, and proofs, has so far only been partially digitized. One major challenge lies in the enormous effort required to compose formal mathematical texts. Such texts can become extremely lengthy, as they must explicitly include every tiny logical step.
For a database of digitized mathematics – or a specific subfield such as number theory or school and university-level mathematics – algorithms could be developed to assist us humans in learning, teaching, and research. The article Die Digitalisierung der Mathematik (engl.: The Digitization of Mathematics) already discussed developments in this area, particularly ambitious projects centered around the younger formal language Lean. The formalization process is indeed making further progress: In July 2023, the Lean Focused Research Organization was founded to advance the “Formal Mathematics Revolution” [5], and Kevin Buzzard was awarded a research grant aimed at formalizing the proof of Fermat’s Last Theorem in Lean within five years [6]. The “Equational Theories Project”, initiated by Terence Tao, is an example of successful online collaboration, where around 22 million implications between algebraic equations were explored in Lean [7]. A major advantage of this approach is that the collaboration is “trustless” – meaning no central trusted authority is required to verify the validity of contributions.
Solving a mathematical problem in formal language can be compared to a game like chess: Mathematics also involves clearly defined moves – logical inferences that allow known statements to be transformed into new ones. The correct and step-by-step application of such inferences is a typical System 2 task, as a sequence of steps is required to coherently and thoroughly derive the solution from axioms or previously proven theorems. (Finding a suitable path to the solution, however, involves creative and intuitive elements – i.e., aspects of System 1.)
DeepMind, the company owned by Google and known for its AIs AlphaGo, AlphaZero, and AlphaFold, developed the AI AlphaProof in 2024 for this purpose. AlphaProof first translates a mathematical problem into Lean using the large language model Gemini. It has taught itself mathematical reasoning similarly to AlphaZero (chess) through reinforcement learning on millions of known mathematical problems. Its self-imposed goal was to tackle the problems of the 2024 International Mathematical Olympiad (IMO). The IMO is an international student competition held annually since 1959. The problems in this competition are anything but easy and require a high degree of creativity. AlphaProof’s solutions scored 28 out of a possible 42 points – equivalent to a silver medal. A gold medal (at least 29 points) was achieved by less than 10% of participants. (Geometric problems were solved by AlphaGeometry, another DeepMind AI specialized in geometry.) One drawback: according to DeepMind, the mathematical problems were initially formalized by hand before being fed to AlphaProof [8].
An IMO gold medal for an AI should soon no longer be a challenge, and even greater goals are already being pursued, such as the expert-level mathematics benchmark FrontierMath [9], [10]. (It is worth noting, however, that a controversy emerged when OpenAI reported a 25% score for its o3 model – only for it to be revealed later that OpenAI had itself been involved in the creation of FrontierMath [11].)
LLMs and the de Bruijn Factor
In his paper [12], F. Wiedijk defines the de Bruijn factor (named after the Dutch mathematician Nicolaas Govert de Bruijn) as the >ratio between the length of a formalized mathematical text and the length of the original, informal version. The author then calculates the de Bruijn factor for three sample texts, each yielding a value of approximately 5.
Let us now define the de Bruijn factor in a more practical sense – as the ratio between the effort (in terms of time) required to write a formal version of a mathematical text and the effort needed for its informal counterpart. In a talk from January 2024 [13], Terence Tao, for example, estimates this factor to be between 10 and 20. However, this value tends to decrease as more formalization groundwork has already been done. Moreover, since the introduction of ChatGPT, LLMs have increasingly supported and often significantly accelerated programming tasks. A dedicated LLM-based tool already exists for Lean as well – the LeanCopilot [14].
The de Bruijn factor will likely continue to decline in the future, raising the intriguing question of whether it might eventually drop below 1 – at least within certain subfields. In that case, writing a formal proof could actually become faster than composing an informal one. Verifying the correctness of such a proof would then require nothing more than a single click.
Even today, a Lean proof can be used to automatically generate a basic LaTeX document or a so-called dependency graph, which visualizes how the proof builds upon other theorems. One might reasonably expect that in such a future scenario, an LLM could also generate a human-readable article at the push of a button. This kind of acceleration in the verification, publication, and communication of mathematical knowledge could represent nothing short of a paradigm shift.
Let’s conclude by giving the floor to ChatGPT, which envisions some of the novel questions that might arise in a future of AI-assisted, formalized mathematics:
- Automatic discovery of new axioms: Can an AI system, by analyzing large amounts of formalized knowledge, propose new, consistent axioms that describe previously overlooked structures in algebra or geometry?
- Formally verified data analysis pipelines: How can statistical methods and machine learning be implemented within formally verified frameworks, so that every result in scientific studies is automatically checked for mathematical correctness?
- AI-driven analysis of proof landscapes: How can formal proof libraries be analyzed with the help of AI systems to identify bottlenecks and gaps in the mathematical literature and to systematically propose new research projects?