Mittlerweile erkennen viele Unternehmen, dass ihren gespeicherten Daten ein Schatz innewohnt. Wenn es nun darum geht, diesen auszugraben und hochwertige Prognosen zu erstellen, haben sich in den vergangenen Jahren maschinelle Lernverfahren zu einem hilfreichen Werkzeug entwickelt. Diese benötigen aber im besten Fall lange Zeitreihen, die nicht immer vorliegen. Wir zeigen Ihnen, wie mit der k-fold blocked cross-validation (BCV) auch diesem Problem Abhilfe geschafft und aus wenigen Zahlen ein Maximum an Informationen generiert werden.
Liebe Besucher des ProgBlogs,
im Zeitalter der Digitalisierung liegen immer größere Mengen an Daten vor, oftmals ohne dass Unternehmen wissen, welches Vorhersagepotenzial diesen innewohnt. Die Herausforderung liegt nämlich nicht darin, Daten einfach nur anzuhäufen, sondern aus diesen sinnvolle Informationen zu extrahieren. Dabei sind Machine-Learning-Verfahren mittlerweile eine große Hilfe. Vereinfacht gesagt erkennen dabei Algorithmen Muster und Trends in einer Datenbasis und können dieses generierte Wissen auf unbekannte Daten anwenden. Für hochwertige Prognosen auf Grundlage dieser Verfahren ist vor allem die Optimierung ihrer Hyperparameter essenziell. Zudem sollten Modellvergleiche die Auswahl von relevanten Kovariaten ermöglichen. Im Idealfall wird so ein Modell generiert, das zukünftige Werte zuverlässig vorhersagt.
Um dieses zu finden, ist es üblich, einen vorliegenden Datensatz in ein Trainings- und ein Testset zu unterteilen. Ersteres wird verwendet, um die Parameter für das Modell zu finden, letzteres, um die Güte des Modells zu überprüfen, also in welchem Maß die Vorhersagewerte des Modells von den tatsächlichen Werten abweichen. Es wird also ein System gesucht, das möglichst gut generalisiert, d. h. eine gute Leistung auf vorher nicht gesehenen Daten abliefert. Je mehr (gut gepflegte) Datenreihen zur Verfügung stehen und je länger diese sind, desto leichter fällt es i. A., ein Modell zu bilden, das diese Eigenschaft gewährleistet.
Der Validierungsprozess bringt Herausforderungen mit sich
Nun ist es leider so, dass die massenhafte Datenspeicherung in vielen Unternehmen oft erst in den letzten Jahren richtig in Fahrt gekommen ist. Deswegen sind die vorhandenen Datenmengen zwar in der Breite groß, haben aber oft nur eine kurze Historie. Allerdings riskiert man mit jedem Wert, der sich im Test- und damit nicht im Trainingsset befindet, wichtige Muster und Trends im Datensatz zu verlieren und ein Modell mit höheren Fehlerwerten zu generieren. Aber genau das ist das Ziel: ein Modell zu finden, das auf neuen Werten robuste Ergebnisse liefert.
Darüber hinaus ist man bei einem klassischen Training/Test-Split darauf angewiesen, dass das Testset möglichst nahe an der “realen Welt” ist und alle Fälle abdeckt, die dem trainierten Modell begegnen könnten. Nehmen wir beispielsweise an, dass Rohölpreise vorhergesagt werden sollen. Als Testset verwenden wir die durchschnittlichen Tagespreise aus dem Dezember eines Jahres und als Trainingsset die vorangegangenen Werte von Januar bis einschließlich November. Sind die Ölpreise im Dezember aufgrund von Saisoneffekten, beispielsweise durch eine erhöhte Nachfrage in den Wintermonaten, deutlich höher als im restlichen Jahr, wird das trainierte Modell im Validierungsprozess einen hohen Fehlerwert haben, obwohl es ansonsten vielleicht gut generalisiert.
Die Kreuzvalidierung schafft Abhilfe
Der Ansatz der Kreuzvalidierung (zu Englisch: cross-validation) nimmt sich diesen Problemen an. Die Methodik nutzt alle vorhandenen Daten sowohl zum Training der Modelle als auch zum Testen. Zum einen können so auch bei relativ kurzen Zeitreihen verlässliche Aussagen getroffen werden, welche Bestandteile ein gutes Modell hat (in Bezug auf Kovariaten und Hyperparameter) und alle wichtigen Muster mit hoher Wahrscheinlichkeit erkannt werden. Zum anderen wird auf diese Weise nicht nur einem einzelnen Testset der große Stellenwert beigemessen, mit dem das Modell steht oder fällt. Diese Art der Validierung ist daher nicht nur auf Daten mit kurzer Historie beschränkt, sondern auch bei längerer Historie sinnvoll einzusetzen.
Trainieren und Testen über Kreuz
Und so funktioniert das Verfahren: Um das beste Set an Hyperparametern und Kovariaten zu finden, wird jede erdenkliche Kombination mit Hilfe der k-fold cross-validation getestet. Man teilt hierbei die Historie der Zeitreihen in k Blöcke. Anschließend wird das Modell auf k-1 Blöcken trainiert und der verbleibende Block mit Hilfe des Modells vorhergesagt. Nimmt man hierbei die ersten k-1 Blöcke zum Trainieren, hat man die klassische Vorgehensweise einer Out-of-Sample-Validierung bei Zeitreihen. Bei der angesprochenen Methode geht man aber noch einen Schritt weiter, um das gesamte Potenzial zu nutzen. Es wird sukzessive der vorherzusagende Block getauscht bis jeder der k Blöcke einmal als Testzeitraum verwendet wurde. Dies gewährleistet, dass eine Abweichung von der Norm in einem Block, welche zu einer Verschlechterung des Modells führen kann, nicht zu sehr ins Gewicht fällt, aber trotz allem Tests auf unbekanntem Terrain stattfinden.
Das Mittel der auf diese Weise gemessenen k Fehler wird verwendet, um den finalen Fehlermesswert zu kalkulieren. Der Satz an Parametern und Kovariaten, der den kleinsten finalen Fehlerwert und somit die beste Vorhersage auf dem gesamten Datensatz geliefert hat, wird dann für zukünftige Prognosen verwendet. Der große Vorteil des Verfahrens ist, dass (fast) jeder Punkt auf dem gesamten Zeitraum einmal out-of-sample vorhergesagt und das maximal mögliche Potenzial des Datensatzes ausgeschöpft wird. Zudem wird durch das Mitteln der Fehler präziser geschätzt und es kann eine genauere Bewertung bezüglich der Generalisierbarkeit des Modells gemacht werden.
Zu beachten ist im Fall von Zeitreihenvorhersagen, dass die Daten aus offensichtlichen Gründen nicht voneinander statistisch unabhängig sind. Dies verletzt allerdings eine der Grundvoraussetzungen der Kreuzvalidierung. Bergmeir und Benítez (2012) stellen daher die k-fold blocked cross-validation (BCV) vor, bei der eine festgelegte Menge an Datenpunkten an den Rändern des als Testset verwendeten Blocks entfernt wird. Durch diesen “Puffer” zwischen Trainings- und Testset kann die Unabhängigkeit der Daten sichergestellt werden.
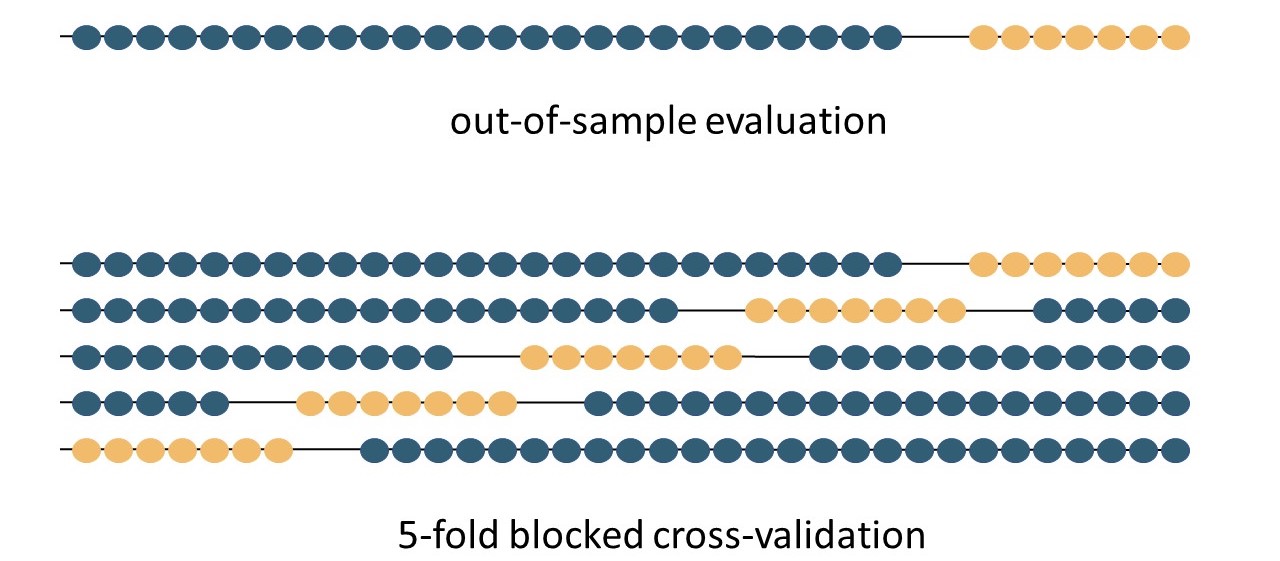
Trainings- und Testsets für traditionelle Out-of-Sample-Evaluation und 5-fold BCV (k=5). Die blauen Punkte sind aus der Zeitreihe des Trainingssets entnommen, die gelben Punkte aus dem Testset. In diesem Beispiel sind an den Rändern der Testset-Blöcke immer zwei Werte ausgelassen (Graphik in Anlehnung an Bergmeir und Benítez (2014)).
Lange Rechendauer zu berücksichtigen
Natürlich fordern die Vorteile der Kreuzvalidierung an anderer Stelle ihren Tribut: Der benötigte Zeitaufwand für die Berechnungen ist nicht zu vernachlässigen und hängt stark von der Menge der Daten und der Wahl von k ab. Beim Vergleich einer einfachen Out-of-Sample-Validierung und einer Kreuzvalidierung wird der klassische Trade-off zwischen Qualität, Zeit und Kosten so ersichtlich: Sind die Zeitreihen lang genug, wird Zeit und Geld gespart. Eine gute Datenbasis wird belohnt. Aber auch wenn sie kurz sind, können wir dennoch Informationen extrahieren, wenn auch mit höherer Berechnungszeit.
Und letztlich ist diese Art der Validierung nicht nur graue Theorie: Sie wurde von uns schon in zahlreichen Projekten zur Vorhersage genutzt und lieferte zuverlässig sinnvolle Ergebnisse.
Interessieren Sie sich für unseren Umgang mit künstlicher Intelligenz?
Infobox:
Hyperparameter: Unter einem Hyperparameter versteht man einen Parameter, der zur Einstellung des Algorithmus bei Machine-Learning-Verfahren dient und nicht durch das Verfahren selbst geschätzt werden kann. Beispielsweise sind dies bei Künstlichen Neuronalen Netzen (KNNs) unter anderem die Anzahl der Epochen, über die trainiert wird oder die Anzahl der Hidden Layers. Die Hyperparameter werden vom Anwender bereits vor dem Trainingsprozess, oft auch manuell, festgelegt.
Kovariate: Unter einer Kovariate versteht man in einem (statistischen) Vorhersagemodell eine Einflussgröße, die als Prädiktor fungiert, also potenziell Einfluss auf die vorherzusagende, abhängige Variable hat und daher in einem Vorhersagemodell berücksichtigt wird. So kann beispielsweise die Tageshöchsttemperatur eine Kovariate für die Modellierung und Vorhersage des täglichen Stromverbrauchs einer Stadt sein.
Literaturnachweis:
Bergmeir, C., & Benítez, J. M. (2012). On the use of cross-validation for time series predictor evaluation. Information Sciences, 191, 192-213.
Bergmeir, C., Costantini, M., & Benítez, J. M. (2014). On the usefulness of cross-validation for directional forecast evaluation. Computational Statistics & Data Analysis, 76, 132-143.
Sie möchten mehr über künstliche Intelligenz und ihr Potenzial erfahren? Nutzen Sie die Vorteile und trauen Sie sich, in Ihr erstes KI-Projekt zu starten:
Jetzt kostenlos E-Book downloaden